Sales ratio study with real data#
AssessPy can easily be used with various data to conduct a sales ratio study. In this vignette, we demonstrate this process using real data from the Cook County Assessor’s Office (CCAO). The CCAO publishes assessments and sales on the Cook County Open Data Portal.
Basics of sales ratio studies#
A sales ratio is the ratio of the assessor’s estimate of a property’s value to the sale price of a property. A sales ratio study is a report on how accurately and fairly an assessor predicted property values. The CCAO has a rigorous set of rules that govern how sales ratios studies are conducted.
In general, there are four important statistics produced in sales ratio studies, listed in the table below. It is important to understand that these statistics are calculated based on properties that sell. In most jurisdictions, the number of properties that sell in any single year is a very small percentage of the overall number of properties. In order to characterize the quality of the assessment role in a jurisdiction, we draw an inference from this small number of properties.
Statistic |
Acceptable Range |
Interpretation |
|---|---|---|
COD |
5 - 15 |
How often properties with the same sale price receive the same predicted market value. Lower CODs indicate more fairness between similarly priced properties. |
PRD |
.98 - 1.03 |
How often properties with different sale prices receive the proportionately different predicted market values. Lower PRDs indicate more fairness between low and high-priced properties. |
PRB |
-.05 - .05 |
PRB is a different approach to measuring fairness across homes with different sale prices. |
Median Assessment Ratio |
.095 - 1.05 |
The median ratio measures whether the most common ratios accurately reflect sale prices |
Sales Chasing (E.4) |
\(\le\) 5% |
Measures the degree to which the statistics above are true reflections of the quality of assessments. |
Interpretation of sales ratio statistics#
Suppose you have a jurisdiction with a median ratio of one and a COD of 20. This indicates that, on average, the assessor predicts the sale price of properties accurately, but with a high dispersion. To use the dart board analogy, the assessor’s darts fall in a wide area centered around the bullseye. On the other hand, if the median ratio is greater than one, and the COD is lower than 10, this indicates that the assessor consistently over-estimates the value of properties in their jurisdiction.
Suppose you have a jurisdiction with a low COD and high PRD & PRB. This indicates that the assessor consistently under-estimates higher value properties, and over-estimates lower value properties. Properties of similar value receive similar estimates, but there is structural inequality in the overall system.
Finally, suppose you have a jurisdiction with CODs, PRDs, and PRBs all within the acceptable range, but there is strong evidence of selective appraisals. In this case, the sales value statistics should be disregarded, since they are based on a non-random selection of the underlying set of properties. They cannot be used to characterize the quality of the assessment role.
Loading data into Python#
There are many ways to load data into Python. Below are some example methods:
jsonlite#
Socrata can also return raw JSON if you manually construct a query URL. Follow the API docs to alter your query. The raw JSON output can be read using the read_json from pandas.
%%capture
import pandas as pd
# Load 100k rows of 2020 residential (major class 2) assessment data
assessments = pd.read_json(
"https://datacatalog.cookcountyil.gov/resource/uzyt-m557.json"
+ "?$where=starts_with(class,'2')&tax_year=2020&$limit=100000"
)
# Load 100k rows of 2020 sales data
sales = pd.read_json(
"https://datacatalog.cookcountyil.gov/resource/wvhk-k5uv.json"
+ "?$where=sale_price>10000&year=2020&$limit=100000"
)
# read_json removes leading zeroes, add them back
assessments.pin = assessments.pin.astype(str).str.zfill(14)
sales.pin = sales.pin.astype(str).str.zfill(14)
From a CSV or Excel#
Python can also read Excel and CSV files stored on your computer.
# CSV files
assessments = pd.read_csv("C:/Users/MEEE/Documents/.... where is your file ?")
sales = pd.read_csv("C:/Users/MEEE/Documents/.... where is your file ?")
# Excel files
assessments = pd.read_excel("C:/Users/MEEE/Documents/.... where is your file ?", sheet_name = "your sheet")
sales = pd.read_excel("C:/Users/MEEE/Documents/.... where is your file ?", sheet_name = "your sheet")
Connecting to a relational database#
The CCAO’s Data Science team uses Amazon Athena. Python can connect to a wide range of database engines.
from pyathena import connect
# Connect to the database
aws_athena_conn = connect(
s3_staging_dir="your-staging-directory",
region_name="your-aws-region"
)
# Fetch data from the SQL server
assessments = pd.read_sql_query("SELECT * FROM your-database.your-table", aws_athena_conn)
Sales ratio study#
In this section, we will use data published on the Cook County Open Data Portal to produce an example sales ratio study.
Prepare the data#
Above, we pulled assessment and sales data from the Open Data Portal. In order to produce our sales ratio statistics, our data needs to be formatted in ‘long form,’ meaning that each row is a property in a given year. The county provides assessed value on the Open Data Portal. For residential properties, we need to multiply assessed value by 10 to get fair market value. Assessment levels can differ for other classes.
# Pivot to longer, Join the two datasets based on PIN, keeping only those that have assessed
# values AND sales
combined = pd.merge(
pd.melt(
assessments.rename(columns={"tax_year": "year"}),
id_vars=["pin", "year", "township_name"],
value_vars=["mailed_tot", "certified_tot", "board_tot"],
var_name="stage",
value_name="assessed",
),
sales[["pin", "year", "sale_price", "is_multisale"]],
on=["pin", "year"],
how="inner",
)
# Remove multisales, then calculate the ratio for each property
# and assessment stage
combined = combined[not combined.is_multisale]
combined["ratio"] = combined.assessed * 10 / combined.sale_price
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
/tmp/ipykernel_1797/2428343520.py in ?()
14 )
15
16 # Remove multisales, then calculate the ratio for each property
17 # and assessment stage
---> 18 combined = combined[not combined.is_multisale]
19 combined["ratio"] = combined.assessed * 10 / combined.sale_price
/opt/hostedtoolcache/Python/3.12.7/x64/lib/python3.12/site-packages/pandas/core/generic.py in ?(self)
1575 @final
1576 def __nonzero__(self) -> NoReturn:
-> 1577 raise ValueError(
1578 f"The truth value of a {type(self).__name__} is ambiguous. "
1579 "Use a.empty, a.bool(), a.item(), a.any() or a.all()."
1580 )
ValueError: The truth value of a Series is ambiguous. Use a.empty, a.bool(), a.item(), a.any() or a.all().
Sales ratio statistics by township#
Cook County has jurisdictions called townships that are important units for assessment. In the chunk below, we calculate sales ratio statistics by township.
import warnings
import numpy as np
import assesspy as ap
warnings.filterwarnings("ignore")
# For each town and stage, calculate COD, PRD, and PRB, and their respective
# confidence intervals then arrange by town name and stage of assessment
town_stats = combined[combined.assessed > 0].copy(deep=True)
town_stats["stage"] = town_stats.stage.astype(
"category"
).cat.reorder_categories(["mailed_tot", "certified_tot", "board_tot"])
town_stats = town_stats.groupby(["township_name", "stage"]).apply(
lambda x: pd.Series(
{
"n": np.size(x["pin"]),
"cod": np.round(ap.cod(ratio=x["ratio"]), 2),
"cod_ci": np.round(ap.cod_ci(ratio=x["ratio"]), 2),
"prd": np.round(ap.prd(x["assessed"], x["sale_price"]), 2),
"prd_ci": np.round(ap.prd_ci(x["assessed"], x["sale_price"]), 2),
"prb": ap.prb(x["assessed"], x["sale_price"], 3),
}
)
)
town_stats["prb_ci"] = town_stats.prb.str["95% ci"]
town_stats["prb"] = town_stats.prb.str["prb"]
town_stats["cod_met"] = town_stats.cod.apply(ap.cod_met)
town_stats["prd_met"] = town_stats.prd.apply(ap.prd_met)
town_stats["prb_met"] = town_stats.prb.apply(ap.prb_met)
town_stats = town_stats[
[
"n",
"cod",
"cod_ci",
"cod_met",
"prd",
"prd_ci",
"prd_met",
"prb",
"prb_ci",
"prb_met",
]
]
town_stats = town_stats[town_stats["n"] >= 70]
town_stats
| n | cod | cod_ci | cod_met | prd | prd_ci | prd_met | prb | prb_ci | prb_met | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| township_name | stage | ||||||||||
| Barrington | mailed_tot | 353 | 22.10 | [20.12, 24.46] | False | 1.04 | [1.02, 1.07] | False | 0.003 | [0.001, 0.004] | True |
| certified_tot | 353 | 22.03 | [20.02, 23.81] | False | 1.05 | [1.02, 1.08] | False | 0.002 | [0.001, 0.004] | True | |
| board_tot | 353 | 20.75 | [18.72, 23.04] | False | 1.05 | [1.02, 1.08] | False | 0.001 | [-0.0, 0.003] | True | |
| New Trier | mailed_tot | 88 | 21.57 | [17.01, 26.59] | False | 1.06 | [1.02, 1.11] | False | 0.003 | [-0.0, 0.007] | True |
| certified_tot | 88 | 22.69 | [17.8, 29.23] | False | 1.08 | [1.03, 1.14] | False | 0.003 | [-0.001, 0.007] | True | |
| board_tot | 88 | 21.66 | [16.93, 26.57] | False | 1.08 | [1.03, 1.13] | False | 0.003 | [-0.001, 0.006] | True | |
| Northfield | mailed_tot | 364 | 18.32 | [16.39, 20.19] | False | 1.03 | [1.02, 1.05] | True | 0.002 | [0.0, 0.003] | True |
| certified_tot | 364 | 18.10 | [16.45, 20.06] | False | 1.03 | [1.01, 1.05] | True | 0.001 | [0.0, 0.003] | True | |
| board_tot | 364 | 17.04 | [15.35, 18.97] | False | 1.05 | [1.03, 1.06] | False | 0.001 | [-0.0, 0.002] | True | |
| Palatine | mailed_tot | 2133 | 15.68 | [14.82, 16.82] | False | 1.01 | [1.0, 1.02] | True | 0.002 | [0.001, 0.003] | True |
| certified_tot | 2133 | 15.62 | [14.57, 17.07] | False | 1.01 | [1.0, 1.01] | True | 0.002 | [0.001, 0.003] | True | |
| board_tot | 2133 | 15.40 | [14.36, 16.47] | False | 1.01 | [1.0, 1.02] | True | 0.002 | [0.001, 0.003] | True | |
| Wheeling | mailed_tot | 2196 | 17.84 | [16.72, 19.29] | False | 1.03 | [1.02, 1.04] | True | 0.002 | [0.001, 0.003] | True |
| certified_tot | 2196 | 17.78 | [16.88, 19.0] | False | 1.03 | [1.02, 1.04] | True | 0.002 | [0.001, 0.002] | True | |
| board_tot | 2196 | 17.55 | [16.45, 19.03] | False | 1.03 | [1.02, 1.04] | True | 0.002 | [0.001, 0.002] | True |
Median ratios by sale price#
Suppose you are concerned that an assessment role is unfair to lower value homes. One way to visually see whether ratios are systematically biased with respect to property value is to plot median ratios by decile. In our sample data, we can see each decile of sale price using the quantile function:
deciles = np.linspace(0.1, 0.9, 9).round(1)
median_ratios = pd.DataFrame(deciles, columns=["Decile"])
median_ratios["Decile"] = (median_ratios.Decile * 100).astype(int).astype(
str
) + "%"
median_ratios["Sale Price"] = np.quantile(combined.sale_price, deciles)
median_ratios["Sale Price"] = median_ratios["Sale Price"].apply(
lambda x: "${:,.0f}".format(x)
)
median_ratios
| Decile | Sale Price | |
|---|---|---|
| 0 | 10% | $130,000 |
| 1 | 20% | $175,000 |
| 2 | 30% | $217,850 |
| 3 | 40% | $257,000 |
| 4 | 50% | $295,000 |
| 5 | 60% | $330,000 |
| 6 | 70% | $378,150 |
| 7 | 80% | $454,600 |
| 8 | 90% | $595,000 |
Using these decile values, we can graph sales ratios across each decile of value. Here, we use the very useful matplotlib package to make an attractive graph.
import matplotlib.pyplot as plt
plt.style.use("default")
warnings.filterwarnings("ignore")
graph_data = combined
graph_data["rank"] = pd.qcut(graph_data["sale_price"], 10, labels=False)
graph_data["rank"] = graph_data["rank"] + 1
graph_data["decile"] = pd.qcut(
graph_data["sale_price"] / 1000, 10, precision=0
)
graph_data["decile"] = graph_data["decile"].astype(str).str.replace("(", "\$")
graph_data["decile"] = graph_data["decile"].str.replace(", ", " - \$")
graph_data["decile"] = graph_data["decile"].str.replace(".0", "K", regex=False)
graph_data["decile"] = graph_data["decile"].str.replace("]", "")
graph_data["decile"] = graph_data["decile"].str.replace(
" - \$9050K", "+", regex=False
)
graph_data = graph_data.groupby(["rank", "decile"]).apply(
lambda x: pd.Series(
{
"Median Sales Ratio": np.median(x["ratio"]),
}
)
)
graph_data = graph_data.reset_index()
plt.scatter(graph_data["decile"], graph_data["Median Sales Ratio"])
plt.xticks(rotation=45)
plt.xlabel("Decile")
plt.ylabel("Ratio")
plt.suptitle("Median Sale Ratios: Open Data Sample", fontsize=14)
plt.title("By decile of sale price in 2020")
plt.gca().set_yticklabels([f"{x:.0%}" for x in plt.gca().get_yticks()])
plt.grid()
plt.show()
Detecting selective appraisals#
Selective appraisal, sometimes referred to as sales chasing, happens when a property is reappraised to shift its assessed value toward its actual sale price. The CCAO requires selective appraisal detection in every sales ratio study. This is because selective appraisal renders all other sales ratio statistics suspect. In the code below, we construct two sets of ratios, one normally distributed, and one ‘chased.’
from statsmodels.distributions.empirical_distribution import ECDF
# Generate fake data with normal vs chased ratios
normal_ratios = np.random.normal(1, 0.15, 10000)
chased_ratios = list(np.random.normal(1, 0.15, 900)) + [1] * 100
# Plot to view discontinuity
ecdf_normal = ECDF(normal_ratios)
ecdf_chased = ECDF(chased_ratios)
plt.plot(ecdf_normal.x, ecdf_normal.y, color="blue")
plt.plot(ecdf_chased.x, ecdf_chased.y, color="red")
plt.xlabel("Ratio")
plt.ylabel("F(x)")
plt.grid()
plt.show()
{
"Blue Chased?": ap.detect_chasing(normal_ratios),
"Red Chased?": ap.detect_chasing(chased_ratios),
}
{'Blue Chased?': np.False_, 'Red Chased?': np.True_}
Ratios that include selective appraisals will be clustered around the value of one much more than ratios produced from a CAMA system. We can see this visually in the graph where the cumulative distribution curve shows a discontinuous jump, or ‘flat spot’, near one.
GINI Coefficient for Vertical Equity#
Another way to measure the vertical equity of assessments is to look at differences in Gini coefficients, a widely used metric to analyze inequality.
The first step in this process is to order the data (ascending) by sale price. Next, calculate the Gini coefficient of sales and assessed values (both ordered by sale price). The difference between these Gini coefficients is known as the Kakwani Index (KI), while the ratio is known as the Modified Kakwani Index (MKI). See this paper for more information on these metrics.
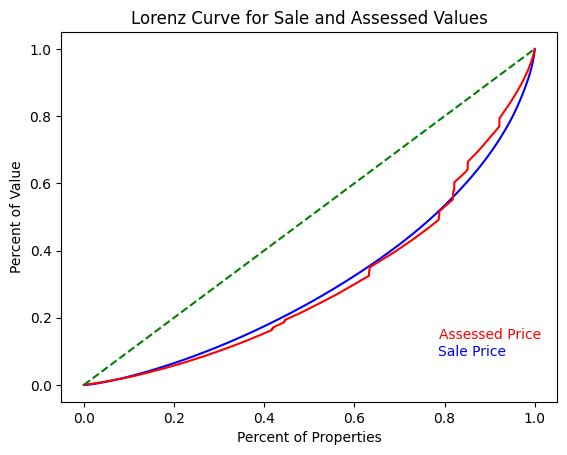
Lorenz curves#
Using the ordered data, you can plot the classic Lorenz curve:
# Combine sale price and assessed value, calculate cumulative sums
gini_data = combined[["sale_price", "assessed"]].sort_values(by="sale_price")
sale_price = gini_data["sale_price"]
assessed = gini_data["assessed"]
lorenz_data_price = pd.DataFrame(
{
"pct": np.concatenate(
([0], np.cumsum(sale_price) / np.sum(sale_price))
),
"cum_pct": np.concatenate(
([0], np.arange(1, len(sale_price) + 1) / len(sale_price))
),
}
)
lorenz_data_assessed = pd.DataFrame(
{
"pct": np.concatenate(([0], np.cumsum(assessed) / np.sum(assessed))),
"cum_pct": np.concatenate(
([0], np.arange(1, len(assessed) + 1) / len(assessed))
),
}
)
# Plot Lorenz curves
fig, ax = plt.subplots()
ax.plot(lorenz_data_price["cum_pct"], lorenz_data_price["pct"], color="blue")
ax.plot(
lorenz_data_assessed["cum_pct"], lorenz_data_assessed["pct"], color="red"
)
ax.plot([0, 1], [0, 1], linestyle="dashed", color="green")
ax.text(0.785, 0.1, "Sale Price", color="blue", va="center")
ax.text(0.9, 0.15, "Assessed Price", color="red", ha="center", va="center")
ax.set_title("Lorenz Curve for Sale and Assessed Values")
ax.set_xlabel("Percent of Properties")
ax.set_ylabel("Percent of Value")
plt.show()
In this graphic, the green line (Line of Equality) represents a hypothetical environment, where property valuations are completely equitable. The axes represent the cumulative percentage of value (y-axis) as the percentage of properties (x-axis) increases.
The curves show that for the vast majority of the income distribution, assessed values are closer to the Line of Equality. This can be interpreted two ways:
When the assessed value curve is above the sale price curve, the gap between the the two lines at any individual point, represents the cumulative over-assessment for all houses at that value or below.
Gini coefficient for sale price is going to be higher than the Gini coefficient for assessed price (larger area between the the curve and the Line of Equality).
In this situation, the graph shows slightly regressive property valuations. This is not immediately intuitive, but to conceptualize this, think of an exaggerated “progressive” policy, where all houses were valued at $0 with one house responsible for all the assessed value. In this distribution, curve would be at 0 until the final house, where it would jump to 100% of the cumulative value (a Gini of 1). Thus, a higher Gini represents more progressive assessments, where tax assessments become larger as property value increases.
KI and MKI#
To translate these curves to a single metric, the Kakwani Index (KI) and Modified Kakwani Index (MKI) are used (as proposed by Quintos). These are straightforward, with the following definitions:
Kakwani Index:
Assessed Gini - Sale Price GiniModified Kakwani Index:
Assessed Gini / Sale Price Gini
from assesspy.utils import check_inputs
# Check inputs
check_inputs(assessed, sale_price)
# Arrange data in ascending order
dataset = list(zip(sale_price, assessed))
dataset.sort(key=lambda x: x[0])
assessed_price = [a for _, a in dataset]
sale_price = [s for s, _ in dataset]
n = len(assessed_price)
# Calculate Gini coefficients
G_assessed = sum(a * (i + 1) for i, a in enumerate(assessed_price))
G_assessed = 2 * G_assessed / sum(assessed_price) - (n + 1)
GINI_assessed = G_assessed / n
G_sale = sum(s * (i + 1) for i, s in enumerate(sale_price))
G_sale = 2 * G_sale / sum(sale_price) - (n + 1)
GINI_sale = G_sale / n
{"MKI": GINI_assessed / GINI_sale, "KI": GINI_assessed - GINI_sale}
{'MKI': 0.9350431709690498, 'KI': -0.02132444068329764}
The output for the Modified Kakwani Index is MKI, and the Kakwani Index is KI. According to the following table, this means that the assessments are slightly regressive.
KI Range |
MKI Range |
Interpretation |
|---|---|---|
< 0 |
< 1 |
Regressive Policy |
= 0 |
= 1 |
Vertical Equity |
> 0 |
> 1 |
Progressive Policy |